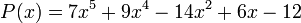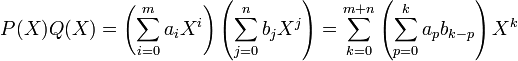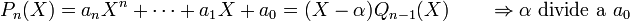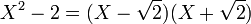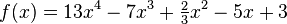Ampliación de matemáticas: noviembre 2010

En matemáticas, se denomina polinomio a la suma de varios monomios (llamados términos del polinomio). Es una expresión algebraica sobre un anillo conmutativo A constituida por un número finito de variables y constantes, utilizando solamente en operaciones de adición, sustracción, multiplicación y potenciación con exponentes de números naturales (es decir, usando sólo las operaciones internas del anillo $\scriptstyle (A,+,\cdot)$ .

Introducción

Por ejemplo:

$x^{2} - 4x + 7 \;$

es un polinomio, sin embargo:

$x^{2} - 4x +7 x^{\frac{3}{2}}, \qquad x^{2} - \frac{4}{x} +7$

no lo son, porque el primero involucra un exponente fraccionario y el segundo divisiones en la variable (una división entre la variable puede interpretarse como una potencia negativa en la variable).

Grado de un polinomio

El polinomio de un sólo término se denomina monomio; el de dos, binomio; el de tres, trinomio; el de cuatro, cuatrinomio o polinomio de "N" términos dependiendo de cuantos haya.

La expresión general de los polinomios que sólo tienen una variable, los más utilizados, es:

$P(x)= a_n x^{n} + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + \cdots + a_2 x^2 + a_1 x + a_0 \,$

por ejemplo:

$P(x)= 7 x^5 + 9 x^4 - 14 x^2 + 6 x - 12 \,$

Se denomina grado de un polinomio a la mayor potencia de los monomios que lo componen.

Historia

Volumen de una pirámide truncada.

La resolución de ecuaciones algebraicas, o la determinación de las raíces de polinomios, está entre los problemas más antiguos de la matemática. Sin embargo, la elegante y práctica notación que utilizamos actualmente se desarrolló a partir del siglo XV.
En el problema 14º del papiro de Moscú (ca. 1890 a. C.) se pide calcular el volumen de un tronco de pirámide cuadrangular. El escriba expone los pasos: eleva al cuadrado 2 y 4, multiplica 2 por 4, suma los anteriores resultados y multiplícalo por un tercio de 6 (h); finaliza diciendo: «ves, es 56, lo has calculado correctamente». En notación algebraica actual sería: V = h (t² + b² + tb) / 3, un polinomio de cuatro variables (V, h, t, b) que, conociendo tres, permite obtener la cuarta variable.
Algunos polinomios, como f(x) = x² + 1, no tienen ninguna raíz que sea número real. Sin embargo, si el conjunto de las raíces posibles se extiende a los números complejos, todo polinomio (no constante) tiene una raíz: ese es el enunciado del teorema fundamental del álgebra.
Hay una diferencia entre la aproximación de raíces y el descubrimiento de fórmulas concretas para ellas. Se conocen fórmulas de polinomios de hasta cuarto grado desde el siglo XVI (ver ecuación cuadrática, Gerolamo Cardano, Niccolo Fontana Tartaglia). Pero, las fórmulas para polinomios de quinto grado fueron irresolubles para los investigadores durante mucho tiempo. En 1824, Niels Henrik Abel demostró que no puede haber fórmulas generales para los polinomios de quinto grado o mayores (ver el teorema de Abel-Ruffini). Este resultado marcó el comienzo de la teoría de Galois que se ocupa del estudio detallado de las relaciones existentes entre las raíces de los polinomios.
La máquina diferencial de Charles Babbage fue diseñada para crear automáticamente tablas de valores de funciones logarítmicas y diferenciales, evaluando aproximaciones polinómicas en muchos puntos, usando el método de las diferencias de Newton.

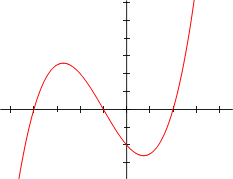
Funciones polinómicas

Las funciones polinómicas son aquellas que surgen de evaluar los polinomios sobre las variables en las que están definidos. Son una clase de funciones suaves, esto es, son infinitamente diferenciables (tienen derivadas de todos los órdenes finitos).
Debido a su estructura simple, los polinomios son muy sencillos de evaluar, y se usan ampliamente en análisis numérico para interpolación polinómica o para integrar numéricamente funciones más complejas. Una manera muy eficiente para evaluar polinomios es la utilización de la regla de Horner.
En álgebra lineal el polinomio característico de una matriz cuadrada codifica muchas propiedades importantes de la matriz. En teoría de los grafos el polinomio cromático de un grafo codifica las distintas maneras de colorear los vértices del grafo usando x colores.

Operaciones con polinomios

Los polinomios se pueden sumar y restar agrupando los términos y simplificando los monomios semejantes. Para multiplicar polinomios se multiplica cada término de un trinomio por el término del otro monomio y se simplifican los monomios semejantes, posteriormente.
Para poder realizar eficazmente la operación tienes que adquirir los datos necesarios de mayor a menor. Una fórmula analítica que expresa el producto de dos polinomios es la siguiente:

$P(X)Q(X) = \left( \sum_{i=0}^m a_i X^i \right) \left(\sum_{j=0}^n b_j X^j \right) = \sum_{k=0}^{m+n} \left(\sum_{p=0}^k a_p b_{k-p} \right) X^k$

Factorización

http://www.youtube.com/watch?v=rlQe_HY9jhk&feature=related

Factorizacioón de polinomios

Para factorizar un polinomio de segundo grado completo (con todos los términos) se divide por el inverso de una de sus raíces sumado con la incógnita, siendo los factores el número por el que dividimos y el resultado; ya que no hay resto, cumpliéndose así que dividendo = inognita - divisor Χ cociente + resto, siendo este el resultado final hayado para completar la ecuación. En caso de que el polinomio no tenga término independiente se sacará la incógnita como factor común y ya está factorizado. También se puede factorizar usando las igualdades notables.
En una anillo conmutativo $\scriptstyle A$ una condición necesaria para que un monomio esa una factor de un polinomio de grado n > 1, es que el término independiente del polinomio sea divisible por la raíz del monomio:

$P_n(X) = a_n X^n + \dots + a_1 X + a_0 = (X-\alpha)Q_{n-1}(X) \qquad \Rightarrow \alpha\ \text{divide a}\ a_0$

Debe tenerse presente que el que un polinomio factorice o no depende de sobre qué anillos se considere la factorización, por ejemplo el polinomio X²-2 no factoriza sobre $\scriptstyle \mathbb{Q}$ pero sí factoriza sobre $\scriptstyle \mathbb{R}$ :

$X^2 - 2 = (X - \sqrt{2})(X + \sqrt{2})$

Por otra parte X²+2 no factoriza ni sobre $\scriptstyle \mathbb{Q}$ , ni tampoco sobre $\scriptstyle \mathbb{R}$ aunque factoriza sobre $\scriptstyle \mathbb{C}$ :

$X^2 + 2 = (X - i\sqrt{2})(X + i\sqrt{2})$

Un cuerpo en el que todo polinomio no constante factoriza en monomios es un cuerpo algebraicamente cerrado.

Ejemplos

Las funciones polinómicas de una variable (x), se corresponden con diversas curvas planas, que se pueden representar en un sistema de coordenadas cartesianas XY.

Polinomio de grado 2: f(x)&n2023 10bsp;= x² - x - 2 = (x+1)(x-2).	Polinomio de grado 3: f(x) = x³/5 + 4x²/5 - 7x/5 - 2 = 1/5 (x+5)(x+1)(x-2).
Polinomio de grado 4: f(x) = 1/14 (x+4)(x+1)(x-1)(x-3) + 0.5.	Polinomio de grado 5: f(x) = 1/20 (x+4)(x+2)(x+1)(x-1)(x-3) + 2.